Category Archive

You are currently browsing the category archive for the ‘ModelWare’ category.

Domain Specific Research Framework using Symbolic Analysis

June 24, 2010 in Exercises illustrating Symbolic Analysis, MDE (Model Driven Engineering), ModelWare, Symbol-Driven-Engineering (SDE) | Leave a comment

We have a definition for scientific symbolic framework at:  https://symbolicanalysis.wordpress.com/2010/06/01/scientific-framework-for-symbolic-analysis/

In this post we use it for a domain specific purpose, for handling a navigator, the software JvnMobileGis.

For analyzing this kind of practical application together with its source, there is a relevant approach in modeling, MDE, and the concepts CIM, PIM and PSM: Computation Independent Model, Platform Independent and Platform Specific Models. Some parts of them are domain specific (DS) and some implementation specifics (IS).

A specific framework for a navigator using symbolic analysis

We define the symbolic analysis framework for navigating in 10 levels as follows:

  1. Ontology is a set of domain specific (DS) concepts for a navigator plus implementation specific (IS) symbols.  Concepts can be regarded as non-grounded higher level symbols. Navigator concepts are the map, the objects, the feature of the object, a road etc. The implementation specific concepts are a menu, a user interface, a database, a socket etc.
  2. Epistemology is a set of transformation rules from concepts to IS symbols. There are two directions: one to develop software and map features to code and another transformation principles how symbols could be connected into concepts. Both transformation directions need some knowledge and they create new knowledge. They describe semantics of each symbol in the ontology.
  3. Paradigm is here reductionist: how to describe ontology and epistemology and the theories and methods as atomic elements. Its “competitor” is holistic approach.
  4. Methodology is a set of theories how ontology will be transformed using epistemology to information, capable of expressing knowledge. There are domain specific theories for the product, the navigator plus implementation specific theories for the software expressed as a symbolic notation.
  5. Method is any way to use the framework in practice. Some methods are for the product, the UI and some for developing software and some for analyzing it.
  6. Tool is a specific means to apply the method in practice. A tool can be any tool, which applies (here) symbolic execution or symbolic analysis, for example for simulating code. The user can work as a tool, too, in order to make something that is impossible for the computer, or something for checking what computer does correctly, or not.
  7. Activity is a human interaction intended for understanding code. The high level types of activities are a) using the product, b)  forward engineering for creating artefacts or c) reverse engineering: finding a bug, browsing code in order to understand some principles etc.
  8. Action is a piece of activity: using the product or forward or reverse engineering.
  9. Sub-action is a part of an action. Lowest sub-actions are primitives like reading an item, making a decision etc.
  10. Lowest level is practical data for the method, tool, activity, action and sub-action. In symbolic analysis practical data can be non-symbolic or symbolic. Non-symbolic data in a program can have any type of the type system of the original source code. Symbolic data can have at most any type in the ontology. It is then very much richer than the non-symbolic notation.

Using the levels 1-10 a complete conceptual framework for any programming language and any operating system and for any application area can be written. There are – as we know – limitations how to ground concepts, but we can model them in many phases using the modeling technology. After the modeling process we can in most cases sharpen our concepts into the symbolic level.

Some links

Petri nets vs Symbolic Atomistic Model

March 28, 2010 in Mathematical formalisms, ModelWare | Leave a comment

A Petri net (also known as a place/transition net or P/T net) is one of several mathematical modeling languages for the description of discrete distributed systems. A Petri net is a directed bipartite graph, in which the nodes represent transitions (i.e. discrete events that may occur, signified by bars), places i.e. conditions, signified by circles, and directed arcs that describe which places are pre- and/or postconditions for which transitions, signified by arrows.

Like industry standards such as UML activity diagrams, BPMN and EPCs, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Petri nets have an exact mathematical definition of their execution semantics, with a well-developed mathematical theory for process analysis.

Because of its executability Petri net is an interesting formalism compared with the symbolic atomistic model.

Formalism for Petri nets

A Petri net consists of places, transitions, and directed arcs. Arcs run from a place to a transition or vice versa, never between places or between transitions. The places from which an arc runs to a transition are called the input places of the transition; the places to which arcs run from a transition are called the output places of the transition.

Places may contain a natural number of tokens. A distribution of tokens over the places of a net is called a marking. A transition of a Petri net may fire whenever there is a token at the end of all input arcs; when it fires, it consumes these tokens, and places tokens at the end of all output arcs. A firing is atomic, i.e., a single non-interruptible step.

Execution of Petri nets is nondeterministic: when multiple transitions are enabled at the same time, any one of them may fire. If a transition is enabled, it may fire, but it doesn’t have to.  Since firing is nondeterministic, and multiple tokens may be present anywhere in the net (even in the same place), Petri nets are well suited for modeling the concurrent behavior of distributed systems.

The following formal definition is loosely based on (Peterson 1981). Many alternative definitions exist.

Syntax

A Petri net graph (called Petri net by some, but see below) is a 3-tuple (S,T,W)\!, where

  • S is a finite set of places
  • T is a finite set of transitions
  • S and T are disjoint, i.e. no object can be both a place and a transition
  • W: (S \times T) \cup (T \times S) \to \mathbb{N} is a multiset of arcs, i.e. it defines arcs and assigns to each arc a non-negative integer arc multiplicity; note that no arc may connect two places or two transitions.

The flow relation is the set of arcs: F = \{ (x,y) \mid W(x,y) > 0 \}. In many textbooks, arcs can only have multiplicity 1, and they often define Petri nets using F instead of W.

A Petri net graph is a bipartite multidigraph (S \cup T, F) with node partitions S and T.

The preset of a transition t is the set of its input places: {}^{\bullet}t = \{ s \in S \mid W(s,t) > 0 \}; its postset is the set of its output places: t^{\bullet} = \{ s \in S \mid W(t,s) > 0 \}

A marking of a Petri net (graph) is a multiset of its places, i.e., a mapping M: S \to \mathbb{N}. We say the marking assigns to each place a number of tokens.

A Petri net (called marked Petri net by some, see above) is a 4-tuple (S,T,W,M_0)\!, where

  • (S,T,W) is a Petri net graph;
  • M0 is the initial marking, a marking of the Petri net graph.

Executablity of Petri nets

Petri nets include a specific logic, with some variations.   Shortly said:

  • firing a transition t in a marking M consumes W(s,t) tokens from each of its input places s, and produces W(t,s) tokens in each of its output places s
  • a transition is enabled (it may fire) in M if there are enough tokens in its input places for the consumptions to be possible, i.e. iff \forall s: M(s) \geq W(s,t).

We are generally interested in what may happen when transitions may continually fire in arbitrary order.

We say that a marking M‘ is reachable from a marking M in one step if M \to_G M'; we say that it is reachable from M if M {\to_G}^* M', where {\to_G}^* is the transitive closure of \to_G; that is, if it is reachable in 0 or more steps.

For a (marked) Petri net N=(S,T,W,M_0)\!, we are interested in the firings that can be performed starting with the initial marking M0. Its set of reachable markings is the set R(N) \ \stackrel{D}{=}\ \{ M' \mid M_0 {\to_{(S,T,W)}}^* M' \}

The reachability graph of N is the transition relation \to_G restricted to its reachable markings R(N). It is the state space of the net.

A firing sequence for a Petri net with graph G and initial marking M0 is a sequence of transitions \vec \sigma = \langle t_{i_1} \ldots t_{i_n} \rangle such that M_0 \to_{G,t_{i_1}} M_1 \wedge \ldots \wedge M_{n-1} \to_{G,t_{i_n}} M_n. The set of firing sequences is denoted as L(N).

Types of different levels of Petri nets are shown below:

Petri net types.

Comparing Petri nets and Symbolic Atomistic Model

Formalism of Petri nets is different from the one of computer programming languages, because in each place there is a contents, which is a set of tokens. The purpose is to study firing and balance between modeling and analyzability.

In spite of the differences, I argue that Petri nets can be converted into the symbolic atomistic model (AHO objects) by some arrangements:

  1. Each place reserves an AHO object.
  2. Each transition reserves so many AHO’s that it requires when the semantics are converted atomistic (atomic formula).
  3. Contents of each place is a separate dynamic AHO – object.
  4. Code for transitions are written in a high level language.
  5. The executing logic will be programmed into the run – methods for AHO’s allowing nondeterminism.
  6. Otherwise, the logic of SimulationWare could be used.

There is no demonstration that it works, but it seems evident that a modified atomistic model (the architecture of AHO’s) should simulate Petri nets, too.

Some links:

Reachability Analysis vs Symbolic Atomistic Model

March 25, 2010 in ModelWare, Other Methodologies | Leave a comment

In graph theory, reachability is the notion of being able to get from one vertex in a directed graph to some other vertex. Note that reachability in undirected graphs is trivial–it is sufficient to find the connected components in the graph, which can be done in linear time.

Definition for Reachability: For a directed graph D = (V, A), the reachability relation of D is the transitive closure of its arc set A, which is to say the set of all ordered pairs (s, t) of vertices in V for which there exist vertices v0 = s, v1, …, vd = t such that (vi – 1, vi ) is in A for all 1 ≤ i ≤ d.

Algorithms for reachability fall into two classes: those that require preprocessing and those that do not. For the latter case, resolving a single reachability query can be done in linear time using algorithms such as breadth first search or iterative deepening depth-first search.

Reachability has many times been modeled using Petri nets.

Producer & Consumer Reachability by Pataricza and Bartha

Because Petri nets can be used for modeling reachability and locks of source code, and the input for it and the symbolic atomistic model (SAM) is the same, too, it is natural to assume, that SAM can be used for modeling reachability and source code locks, too.

In fig above the different slices (parts of the graph) could be symbolic models captured from methods of threads of Java or C++ or other code. Typically some threads are consumers and some producers.

It is straightforward to visualizate logic of threads using the symbolic atomistic model as a base so that crtical resources can be seen as connective nodes between different parts of the threads.

Some links:

Reaching Highest Granularity Models and Simulation

March 17, 2010 in ModelWare | Leave a comment

Granularity is the extent to which a system is broken down into small parts, either the system itself or its description or observation. It is the “extent to which a larger entity is subdivided. For example, a yard broken into inches has finer granularity than a yard broken into feet.

Coarse-grained systems consist of fewer, larger components than fine-grained systems; a coarse-grained description of a system regards large subcomponents while a fine-grained description regards smaller components of which the larger ones are composed.

The terms granularity, coarse and fine are relative, used when comparing systems or descriptions of systems. An example of increasingly fine granularity: a list of nations in the United Nations, a list of all states/provinces in those nations, a list of all counties in those states, etc.

In physics a fine-grained description of a system is a detailed, low-level model of it. A coarse-grained description is a model where some of this fine detail has been smoothed over or averaged out. The replacement of a fine-grained description with a lower-resolution coarse-grained model is called coarse graining.

In molecular dynamics, coarse graining consists in replacing an atomistic description of a biological molecule with a lower-resolution coarse-grained model that averages or smooths away fine details. Coarse-grained models have been developed for investigating the longer time- and length-scale dynamics that are critical to many biological processes, such as lipid membranes and proteins.

In parallel computing, granularity means the amount of computation in relation to communication, i.e., the ratio of computation to the amount of communication. Fine-grained parallelism means individual tasks are relatively small in terms of code size and execution time.

The granularity of data refers to the fineness with which data fields are sub-divided. For example, a postal address can be recorded, with low granularity, as a single field:

  1. address = 200 2nd Ave. South #358, St. Petersburg, FL 33701-4313 USA

or with high granularity, as multiple fields:

  1. street address = 200 2nd Ave. South #358
  2. city = St. Petersburg
  3. postal code = FL 33701-4313
  4. country = USA

About granularity of computer models

Granularity can easily be defined for computer models like source code models including UML, abstract syntax tree, MOF, MDE, ADM, XML etc.  It is not clear what is the granularity of typical AST – implementations, because AST is often an abstraction about a computer language. Hence, granularity and abstraction has many common things, they are counterexamples.

In granular computing there are principles for studying variables.  One typical class of variable granulation methods derive more from data clustering methodologies than from the linear systems theory informing the above methods (see picture below).

About granularity of symbolic atomistic model and SDE

Symbolic atomistic model is by far the highest granular model to describe source code and its behavior. It models orginal code symbols as AHO – hybrid objects, although their commands are abstractions made by predicates, they don’t miss any information. That is excellent and provides reversibility to convert an internal model into the original code backwards. In simulation it models interpretations between symbols and creates side effects which are results from any computation from any symbol. Hence, the output of the simulation process is as fine granular as the original symbols. It provides excellent ways to study program execution. On the other side, there can appear too much information for a long run, therefore there should be ways to limit information captured from simulation.

Some links:

Executable UML vs Automata Theory vs Symbol-Driven Engineering

February 19, 2010 in ModelWare, Other Methodologies, SimulationWare, Symbol-Driven-Engineering (SDE) | Leave a comment

Executable UML, often abbreviated to xtUML or xUML, is the evolution of the Shlaer-Mellor method to UML. Executable UML graphically specifies a system using a profile of the UML. The models are testable, and can be compiled into a less abstract programming language to target a specific implementation. Executable UML supports MDA through specification of platform-independent models, and the compilation of the platform-independent models into platform-specific models.

Executable UML is used to model the domains in a system. Each domain is defined at the level of abstraction of its subject matter independent of implementation concerns. The resulting system view is composed of a set of models represented by at least the following:

  • The domain chart provides a view of the domains in the system, and the dependencies between the domains.
  • The class diagram defines the classes and class associations for a domain.
  • The statechart diagram defines the states, events, and state transitions for a class or class instance.
  • The action language defines the actions or operations that perform processing on model elements.

Shortcomings of Executable UML

UML doesn’t define semantics of a programming language. Hence, it is not complete to describe behavior of any exact system. In order to correct this shortcoming some new principles are needed. Some of them are: automata theory and symbol-driven engineering.

Automata Theory and Symbol-Driven Engineering (SDE)

Automata theory defines behavior model for corresponding code elements. Therefore, this theory background  eliminates the gap between program behavior and the corresponding model, like UML

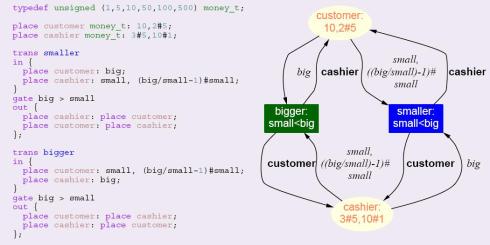
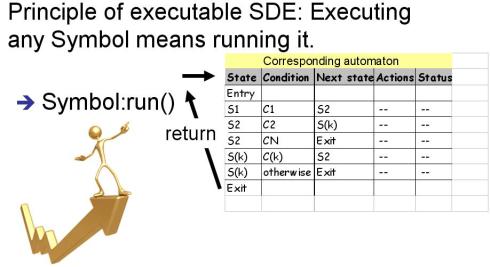
In SDE every symbol has an automaton behind it. In order to execute those symbols an invocation Symbol:run is needed plus some specific initailizations for some specific symbols like definitions (method invocations and  object and variable definitions). See figure below.

Some links:

Round-Trip Engineering vs. Symbolic Analysis

February 17, 2010 in GrammarWare, ModelWare, Other Methodologies | Leave a comment

Round-trip engineering is a functionality of software development tools that provides generation of models from source code and generation of source code from models; this way, existing source code can be converted into a model, be subjected to software engineering methods and then be converted back.

Round trip is a particular model perspective in the UML standard, and it covers conceptual elements of the full execution use case that happens in an implemented system. This includes the network communication, in typical web-based applications.

Round-trip engineering vs. Symbolic Analysis

When rount-trip engineering creates typical UML models from code, Symbolic analysis instead creates symbolic atomistic models from code: from GrammarWare to ModelWare.

Some links:

Maximum Expressive Power with Minimal Construction

December 19, 2009 in GrammarWare, MaintenanceWare, ModelWare, Other Methodologies | 1 comment

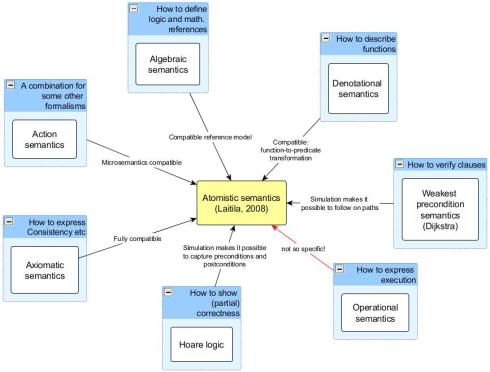
In this story we start from the known definition for Expressive power to extend its scope to semantics programming languages, which have numerous ways to express the specific meanings (below 8 formalismis are listed) of tems of languages. We suggest that (near) all of these semantic principles can be combined in the atomistic semantics, which is a novel hybrid construction, a high-abstraction way to simulate source code.

What is Expressive power

Expressive power is in computer science a feature of a language, which refers to: 

  • what can be said in the language (at all)
  • how concisely it can be said.

Formal discussions mostly use the term in the first sense, leaving conciseness as a less important factor. This is the case in areas of mathematics that deal with the exact description of languages and their meaning, such as formal language theory, mathematical logic and process algebra.

In informal discussions, the term often refers to the second sense, or to both. This is often the case when discussing programming languages. Efforts have been made to formalize these informal uses of the term [2].

The notion of expressive power is always relative to a particular kind of thing that the language in question can describe, and the term is normally used when comparing languages that describe the same kind of things, or at least comparable kinds of things.

The design of languages and formalisms involves a trade-off between expressive power and analyzability. The more a formalism can express, the harder it becomes to understand what instances of the formalism say. Decision problems become harder to answer or completely undecidable.

Formal language theory mostly studies formalisms to describe sets of strings, such as context-free grammars and regular expressions. Each instance of a formalism, e.g. each grammar and each regular expression, describes a particular set of strings. In this context, the expressive power of a formalism is the set of sets of strings its instances describe, and comparing expressive power is a matter of comparing these sets.

An important yardstick for describing the relative expressive power of formalisms in this area is the Chomsky hierarchy.

Expressive power means one quality attribute of programming language semantics

There are some ways to describe expressive power of each language term (e.g. clause).

1) Axiomatic semantics

  • Axiomatic semantics define the meaning of a command in a program by describing its effect on assertions about the program state. The assertions are logical statements – predicates with variables, where the variables define the state of the program.

2) Algebraic semantics

  • In logic, algebraic semantics is a formal semantics based on algebras.

3) Operational semantics

4) Denotational semantics

  • Denotational semantics is concerned with finding mathematical objects called domains that represent what programs do. For example, programs (or program phrases) might be represented by partial functions, or by Actor event diagram scenarios, or by games between the environment and the system

5) Action semantics

  • Action semantics is an approach that tries to modularize denotational semantics, splitting the formalization process in two layers (macro and microsemantics) and predefining three semantic entities (actions, data and yielders) to simplify the specification

6) WP-semantics / Predicate transformer semantics

  • Predicate transformer semantics is an extension of Floyd-Hoare Logic invented by Dijkstra and extended and refined by other researchers. It was first introduced in Dijkstra’s paper “Guarded commands, nondeterminacy and formal derivation of programs”. It is a method for defining the semantics of an imperative programming language by assigning to each command in the language a corresponding predicate transformer. A predicate transformer is a total function mapping between two predicates on the state space of a program.
  • The canonical predicate transformer of sequential imperative programming is the so-called “weakest precondition” wp(S,R). Here S denotes a list of commands and R denotes a predicate on the space, called the “postcondition“. The result of applying this function gives the “weakest pre-condition” for S terminating with R true. An example is the following definition of the assignment statement:
wp(x := E, R)\ =\ R_E^x

This gives a predicate that is a copy of R with the value of x replaced by E.

  • Refinement calculus is a formalized approach to stepwise refinement for program construction. The required behaviour of the final executable program is specified as an abstract and perhaps non-executable “program”, which is then refined by a series of correctness-preserving transformations into an efficiently executable program.

7) Hoare’s axiomatic semantics e.g. Hoare logic

  • Hoare logic (also known as Floyd–Hoare logic or Hoare rules) is a formal system with a set of logical rules for reasoning rigorously about the correctness of computer programs. It was proposed in 1969 by the British computer scientist and logician C. A. R. Hoare, and subsequently refined by Hoare and other researchers. The original ideas were seeded by the work of Robert Floyd, who had published a similar system for flowcharts.
  • The central feature of Hoare logic is the Hoare triple. A triple describes how the execution of a piece of code changes the state of the computation. A Hoare triple is of the form
\{P\}\;C\;\{Q\}
where P and Q are assertions and C is a command. P is called the precondition and Q the postcondition: if the precondition is met, the command establishes the postcondition. Assertions are formulas in predicate logic.

8) Atomistic semantics

Atomistic semantics is a hybrid construction, whose expressive power comes from Prolog, a first order predicate logic extended for logic programming. Its type system is rich in expressing any axiomatic feature. The other side of that semantics is object-oriented. That makes it possible to define algebraic equations, formulas or any dependendies using object handles and their static counterparts, tree-based Prolog references, as the base.

There is no research to compare atomistic semantics with denotational semantics, but there are many comparisons between Lisp and Prolog. They are rather compatible to express complicated models and functions, even Lisp is more generic in expressing meta-features. The latter one is not important in expressing features from source code (when ignoring macros and precompilers).

Operational semantics is the hardest one, having two levels.

Below our summary as a picture.

Expressive power of a formalism

If two formalisms have equal power, then it is possible to express same kind of methods (working practices from the user point-of-view) using tools of the corresponding formalisms. In program comprehension (PC) there are multiple needs for the user to do: to define hypotheses, to learn structures, to navigate, to understand behavior, to prove correctness and to simulate and evaluate specific expressions. Therefore, for so many different purposes of program comprehension, atomistic semantics is a remarkable suggestion.

Some links:

Differences from ADM’s KDM to the Atomistic Symbolic Model

December 16, 2009 in ModelWare, Other Methodologies, Transformation Framework | 1 comment

Architecture Driven Modernization (ADM)

ADM –Standards have been introduced in Architecture-Driven Modernization (ADM) Task Force: Overview, Scenarios & Roadmap  (see  here, page 7).

Why ADM?

It is a process of understanding & evolving existing software assets for:

  • Software improvement
  • Modifications
  • Interoperability
  • Refactoring
  • Restructuring
  • Reuse
  • Porting
  • Migration
  • Translation into another language
  • Enterprise application integration
  • Service-oriented architecture

Modernization starts where existing practices fail to deliver against business objectives

  • RFP #1: ADM: Knowledge Discovery Meta-Model (KDM) Package
  • RFP #2: ADM: Abstract Syntax Tree Meta-Model (ASTM) Package
  • RFP #3: ADM: Analysis Package
  • RFP #4: ADM: Metrics Package
  • RFP #5: ADM: Visualization Package
  • RFP #6: ADM: Refactoring Package
  • RFP #7: ADM: Target Mapping & Transformation Package

There are 12 modernization scnerios in ADM (see page 9).

Differences between the Atomistic Model and ADM

The differences are below:

ADM’s packages Implementation in the Atomistic Model
RFP #1: ADM: Knowledge Discovery Meta-Model (KDM) Package This information (RFP #1) is in the model (see AHO), the Symbolic notation
RFP #2: ADM: Abstract Syntax Tree Meta-Model (ASTM) Package This info has the Symbolic notation, it lies in AHOs
RFP #3: ADM: Analysis Package Simulation has been implemented using the run method of AHO
RFP #4: ADM: Metrics Package There is currently no correspondence
RFP #5: ADM: Visualization Package These are graphs generated from AHOs
RFP #6: ADM: Refactoring Package There is currently no correspondence
RFP #7: ADM: Target Mapping & Transformation Package There is currently no correspondence, but transformation from Symbolic to the input language and back has been done in an external Transformation Framework

The principles are then quite different. An atomistic model is really atomistic, not holistic.

Some links:

Predicate Abstraction (Microsoft SLAM) vs Symbolic Analysis

December 12, 2009 in Model Checking, ModelWare | Leave a comment

The SLAM project, which was started by Microsoft Research, aimed at verifying some software safety properties using model checking techniques. It is implemented in Ocaml, and has been used to find many bugs in Windows Device Drivers. It is distributed as part of the Microsoft Windows Driver Foundation development kit as the Static Driver Verifier (SDV).

SLAM uses a technique called counterexample-guided abstraction refinement, which uses progressively better models of the program under test.

“SLAM originally was an acronym but we found it too cumbersome to explain. We now prefer to think of ‘slamming’ the bugs in a program.” It probably stood for “Software, Languages, Analysis, and Modeling.” Note that Microsoft has since re-used SLAM to stand for “Social Location Annotation Mobile”

About Abstraction Methods:

There are three ways to abstract programs.

  1. Over-abstract like abstract interpretation
  2. Under-abstraction like SLAM, also called meat-axe – abstraction, which cuts of some information
  3. Precise abstraction which is the best description for Symbolic Analysis (Laitila), which uses the Symbolic language for that.

Because SLAM removes some information, it is not complete to describe program comprehension features of the program, which include: control flow, data flow, state flow, operations and full functionality (Pennington, Wiedenbeck, von Mayrhauser et al.).

Paper X describes counterexample-guided abstraction refinement with some methods:

There is a traffic light example in it to model states.

Some algorithms in the paper are SPLITPath, PolyRefine and SPLITLoop.

Precice abstraction in Symbolic Analysis

We define precise abstraction as a formula M <– –> M’, where M is the original model (or code) containing Java, C++ or other language and M’ is the abstracted model with AHO objects, where the command from each AHO has been transformed according to the original grammar term of the corresponding program element. The abstracted model can be transformed back into the original language. Thus, the model is reversible.

Some links:

Borrowing the Functionaly of the Kripke Structure for Atomistic Model

November 29, 2009 in Model Checking, ModelWare, SimulationWare | Leave a comment

A Kripke structure is a type of nondeterministic finite state machine used in model checking to represent the behaviour of a system. It is basically a graph whose nodes represent the reachable states of the system and whose edges represent state transitions. A labeling function maps each node to a set of properties that hold in the corresponding state. Temporal logics are traditionally interpreted in terms of Kripke structures.

Let AP be a set of atomic propositions, i.e. boolean expressions over variables, constants and predicate symbols.

A Kripke structure is a 4-tuple M = (S,\; I,\; R,\; L) consisting of

  • a finite set of states S\;
  • a set of initial states I \subseteq S
  • a transition relation R \subseteq S \! \times \! S \; where \; \forall s \! \in \! S, \; \exist s^' \!\! \in \! S such that (s,s^') \in R
  • a labeling (or interpretation) function L: S \rightarrow 2^{AP}

Since R is left-total, it is always possible to construct an infinite path through the Kripke structure. Thus a deadlock state has a single outgoing edge back to itself.

The labeling function L defines for each state s ∈ S the set L(s) of all atomic propositions that are valid in s. In the Kripke structure, the transition function should be complete,i.e each and every state should have transition.In other words there should not be any dead states in the graph.

Combining the Semantics of the Atomistic Model and the Kripke Structure with each other

If we use the notation of the Kripke structure for the Atomistic Model we get the definitions:

The atomistic model is a Kripke structure,  a 4-tuple M = (S,\; I,\; R,\; L) consisting of

  • a finite set of  states S\; implemented as symbols in the model illustrating clauses of the original clause and side effects caused by the simulation/evaluation processes.
  • a set of initial states I \subseteq S implemented as symbols of the models: either clauses or side effects.
  • a transition relation R \subseteq S \! \times \! S \; where \; \forall s \! \in \! S, \; \exist s^' \!\! \in \! S such that (s,s^') \in R implemented as links of the symbols.
  • a labeling (or interpretation) function L: S \rightarrow 2^{AP} implemented as a command-fact in each symbol.

Summary about the correspondece

The atomistic model is downwards compatible with the Kripke structure. It leads to a conculsion (by inspection) that all functions and mathematical processes intended for the Kripke structure, e.g. model checking, can be borrowed for the use of the atomistic model. Only a simple transformation is needed.

Some links:

Erkki Laitila, PhD (2008) computer engineer (1977)